Est-ce que la topologie peut nous sauver ?#

Date de publication initiale : 15 août 2024

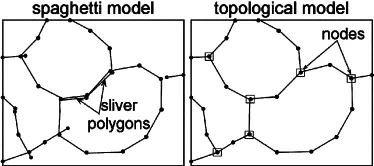
Dans les SIG, on distingue souvent deux types de modèles pour représenter les données spatiales : le modèle « spaghetti » et le modèle topologique.

• Spaghetti : dans un système de type spaghetti, les entités géographiques sont stockées et gérées individuellement, sans relations explicites entre elles. Chaque ligne ou polygone est dessiné sans tenir compte d'autres éléments qui pourraient se toucher ou se chevaucher. Cela peut conduire à des incohérences, comme des doublons de lignes ou des intersections non gérées, ce qui complique les analyses spatiales et peut réduire la précision des résultats.

• Topologie : à l'inverse, la topologie dans QGIS (ou dans tout autre SIG supportant ce modèle) s'assure que les entités spatiales sont stockées avec des règles qui définissent et maintiennent les relations spatiales entre les entités. Par exemple, deux polygones adjacents partageront une ligne commune sans duplication, et les intersections seront gérées correctement. La gestion topologique aide à prévenir les erreurs géométriques, améliore la précision des analyses et facilite la maintenance des données.

Non, ce n'est toujours pas ici que je ferai l'article sur la topologie. Au mieux, cela sert de teaser.

Cet article est la cinquième partie de la série d'été sur la gestion de la géométrie dans les SIG.

Le dossier 4 : les bases de données relationnelles

Commenter cet article

Retour sur GRASS#

L'une des caractéristiques de GRASS est sa gestion topologique des données vectorielles. Contrairement à d'autres systèmes qui utilisent un modèle de données « spaghetti », où les entités géométriques sont stockées sans considération explicite des relations spatiales entre elles, GRASS maintient une structure topologique stricte.

Overlap pour une meilleure sélection dans GRASS#

Dans la partie précédente, j'ai indiqué qu'il y avait une autre façon de faire du v.select. En effet, on a utilisé GEOS avec intersects.

La documentation de GRASS mentionne un autre opérateur overlap, celui par défaut et utilisant les fonctions GRASS natives. Quel est le résultat ?

Oui, celui que l'on attend ! Enfin ! Tant sur la base que sur la line, les points d'intersection intersectent bien les géométries d'origine !

Utilisation de v.clean#

Mais, comme GRASS est topologique, on peut également s'en servir pour retrouver nos intersections. Pour cela, on va réaliser un petit hack pour simplifier nos calculs.

Pour utiliser la topologie, nous allons faire l'union de nos deux lignes de base et line pour ensuite nettoyer celles-ci. Le nettoyage, via v.clean se fera seulement avec l'outil break. L'utilisation de l'outil break de v.clean dans ce cas précis sert à « nettoyer » les données en réalisant une opération topologique :

Que fait la fonction break ?

• Cela découpe les lignes à leurs points d'intersection.
• Cela crée de nouveaux nœuds aux endroits où les lignes se croisent.

On parle de nettoyage, car, initialement, les lignes de base et line se croisent sans être réellement connectées topologiquement. Le « nettoyage » consiste à établir une véritable connexion topologique à ces intersections.

Dans notre cas, en appliquant « break » après l'union des lignes, on force GRASS à reconnaître et à matérialiser les points d'intersection ; cela transforme de simples croisements géométriques en nœuds topologiques explicites.

Cela permet d'exploiter ensuite la structure topologique de GRASS pour identifier facilement ces points d'intersection.

Ainsi, nous allons passer de :

à

Maintenant, on regarde si notre fonction v.select avec intersects fonctionne.

Hourra !

Quels sont les points ? Les mêmes que jusqu'à présent. Mais, alors, que s'est-il passé ? Eh bien, revenons sur QGIS et expliquons cela graphiquement.

De la topologie dans QGIS#

Dans QGIS, il existe un mode d'édition que j'affectionne particulièrement, qui est… l'édition topologique.

Le stockage dans QGIS est dit « spaghetti ». Les données sont toutes dans ce plat de pâtes : les entités géographiques sont stockées individuellement sans relations topologiques explicites. Mais, bien que QGIS utilise un modèle de données de type « spaghetti », le logiciel propose des outils qui aident à maintenir la cohérence géométrique entre les couches.

En particulier, ici, nous allons utiliser la fonction d'édition topologique, qui, lors de chaque accrochage sur un segment, va ajouter des nœuds sur le segment accroché.

La couche base_topology est une copie de base sur laquelle j'ai dessiné, avec l'édition topologique, la couche test_line.

Si l'on refait notre test de « sélection par localisation » avec le prédicat « intersects », nous avons nos 34 lignes de sélectionnées.

Pour être certain que ce n'est pas juste des sommets qui seraient de l'autre côté de la ligne, on peut les extraire et refaire l'opération.

La topologie est grande, la topologie est bonne, elle va sauver nos calculs !

Les limites de la topologie#

Oui, la topologie c'est très bien, et son utilisation dans QGIS, via ses outils ou via GRASS, est très puissante. Mais, l'on peut faire quelques reproches :

• plus difficile à utiliser/à maintenir ;
• traitements plus longs lors d'intégrations de données externes, non topologiques ;
• nombre de sommets plus important ;
• modification de la donnée d'origine ;
• etc.

En particulier, j'expliquerai bientôt ce que j'indique par « modification de la donnée d'origine ».

Dans la première partie, j'ai écrit que la distance du point par rapport à la géométrie d'origine était proche de zéro, mais pas exactement 0.

Avec l'édition topologique de QGIS ou le stockage de GRASS, les points d'intersections coïncident avec les sommets de nos géométries, merci à la topologie.

Toutefois, en dehors des nœuds ajoutés, est-ce que notre géométrie est la même ? Visuellement, encore une fois, hormis les nœuds, cela semble identique.

Comparons les angles des segments.

Dans notre géométrie d'origine, nous avons quatre segments, avec comme azimut, en radians :

Soit, en partant du bas gauche et en tournant dans le sens horaire :

• 4.341309933406307
• 1.0434054052601267
• 2.401617769614756
• 5.848325554504713

Dans notre base qui a été éditée topologiquement ?

Sur le premier segment d'origine :

• 4.341309933414985
• 4.3413099333929175
• 4.341309933355925
• 4.341309933411935
• 4.34130993343072
• 4.341309933414806
• 4.341309933388343
• 4.341309933497785
• 4.341309933391953

Le deuxième :

• 5.848325554496416
• 5.848325554486275
• 5.8483255545512725
• 5.848325554512849
• 5.848325554487155
• 5.848325554478932
• 5.848325554530697
• 5.848325554523524
• 5.848325554479168

Le troisième :

• 1.0434054052235737
• 1.043405405251191
• 1.0434054052730521
• 1.0434054052793966
• 1.0434054052156936
• 1.0434054052777524
• 1.043405405257653
• 1.0434054052902961
• 1.0434054052482782

Le quatrième :

• 2.401617769621854
• 2.401617769590059
• 2.4016177695994174
• 2.4016177696075154
• 2.401617769638797
• 2.401617769583275
• 2.4016177696211147
• 2.401617769630777
• 2.4016177696067103
• 2.4016177696313

Les nouveaux segments ne sont pas « alignés » comme le segment d'origine. De rien du tout, en vrai, car si on convertit ces angles en degrés, on obtient 4 valeurs, identiques à nos segments d'origine :

• 335.084
• 59.783
• 137.603
• 248.739

En réalité, pas totalement, mais j'ai volontairement arrondi à trois chiffres après la virgule. Pourquoi ai-je fait ça ? Marre de me trimbaler autant de chiffres. Et, puis, est-ce vraiment utile d'avoir autant de chiffres après la virgule ?

6 : beyond the comma avec SFCGAL

Auteur·ice#

Loïc Bartoletti#

Après un cursus en Histoire, je me suis orienté vers l'urbanisme sur l'aménagement des territoires.

J'ai travaillé pendant environ 10 ans dans une station touristique dans les Alpes, Megève, en tant qu'urbaniste puis responsable du bureau d'études et administrateur SIG.

Bidouilleur et partisan des solutions OpenSource, j'ai commencé à toucher à GRASS, puis QGIS et PostGIS. Au fil du temps j'ai contribué à ces logiciels, principalement pour migrer des outils DAO vers le SIG et je suis aujourd'hui commiter QGIS, PostGIS et FreeBSD où je m'occupe des paquets des outils OSGeo et plus si affinité.

Licence Beerware #

Ce contenu est sous licence Beerware (Révision 42).
Les médias d'illustration sont potentiellement soumis à d'autres conditions d'utilisation.

Commentaires