GEOS au cœur de QGIS#

Date de publication initiale : 25 juillet 2024

Dans la partie précédente, nous avons posé le problème : le résultat d'une intersection n'intersecte pas toujours la donnée d'origine. Cette réalité peut surprendre les nouveaux utilisateurs de SIG et frustrer les plus expérimentés qui cherchent une précision dans leurs analyses spatiales.

Dans cette section, nous allons plonger dans les dessous des SIG en explorant le fonctionnement de ces traitements. Nous nous concentrerons en particulier sur le rôle de GEOS dans QGIS.

Cet article est la deuxième partie de la série d'été sur la gestion de la géométrie dans les SIG.

Le dossier 1 : Constat : les calculs

Commenter cet article

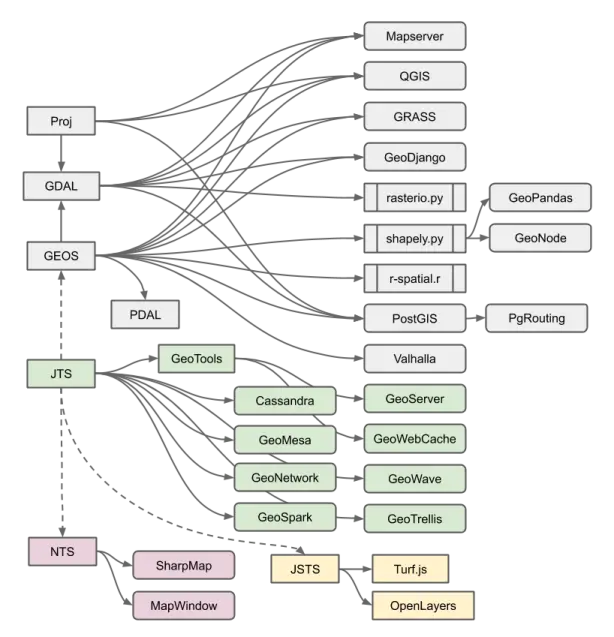
Qu'est-ce que GEOS ?#

GEOS (Geometry Engine - Open Source) est une bibliothèque C++ qui fournit des fonctions de calculs sur les géométries Simple Feature OGC. Elle est largement utilisée dans divers outils SIG, y compris QGIS, pour effectuer des calculs géométriques. GEOS est une implémentation de l'API de JTS (Java Topology Suite) qui vise à manipuler des géométries planes en 2D.

Source : Performance Improvements in GEOS, Paul Ramsey (2021, Crunchy Data)

Le rôle de GEOS dans QGIS#

Dans QGIS, GEOS joue un rôle crucial dans le traitement des données géographiques. Il est particulièrement utilisé pour évaluer les prédicats spatiaux tels que intersects, touches, disjoint, etc. Ces prédicats sont essentiels pour déterminer les relations spatiales entre différentes géométries.

Pour les connaisseurs du code de QGIS, il est vrai que certains traitements ne sont pas réalisés par GEOS, mais par QGIS. Nous regarderons cela dans la partie sur l'étude des algorithmes, mais en soi, cela ne change pas grand-chose au problème.

Utilisation de GEOS sans QGIS#

Si vous ne le savez pas, il est également possible de réaliser des calculs directement avec GEOS, sans utiliser l'interface graphique de QGIS. Une des façons de faire cela est d'utiliser geosop, un outil en ligne de commande qui permet de manipuler des géométries avec les fonctions de GEOS.

geosop permet aux utilisateurs d'exécuter des opérations complexes sur les géométries grâce à des commandes simples. Par exemple, pour vérifier si une géométrie en intersecte une autre, on peut utiliser la commande suivante :

> geosop -a "LineString(0 0, 10 10)" -b "Point(5 5)" intersects
true
> geosop -a "LineString(0 0, 10 10)" -b "Point(5 4)" intersects
false

Ici, nous avons utilisé le format WKT³ pour tester si les géométries a et b s'intersectent. Par la suite, on ajoutera et expliquera d'autres options au fur et à mesure de nos utilisations.

Testons notre cas directement avec GEOS#

Pour rappel, nos géométries sont les suivantes :

base : 0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341
line : 010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341

Pour se faire la main, on va tester si nos géométries s'intersectent bien. On ne l'avait pas testé sur QGIS, mais cela semble évident.

> geosop \
-a \
"0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341" \
-b \
"010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341" \
intersects

Tip

Ici, j'ai utilisé \ pour que la commande soit sur plusieurs lignes afin de simplifier la lecture de la commande ; vous pouvez évidemment tout faire sur une ligne.

Le résultat retourné est true. C'est cohérent.

Maintenant, nous allons calculer l'intersection. Pour cela, on utilise l'opérateur intersection au lieu de intersects, rien de compliqué.

> geosop \
-a \
"0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341" \
-b \
"010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341" \
intersection

La réponse est MULTIPOINT ((1981640.7849060092 5199258.022088398), (1981583.6205737416 5199333.301878075))

Ah ! C'est une petite différence avec QGIS qui retourne deux points. Ici, GEOS retourne un MULTIPOINT, qui, selon moi, est plus cohérent, mais qu'importe. Le WKT est plus lisible, mais il a l'inconvénient de ne pas toujours avoir la même représentation. QGIS nous retourne 17 décimales et GEOS : 10 ; ce qui, dans tous les cas, est déjà trop pour du projeté, on en reparlera plus tard.

Afin d'éviter ces différences, nous allons travailler avec le WKB. Pour le récupérer, on ajoute simplement l'option WKB à l'option -f pour le format de sortie :

> geosop \
    -a \
    "0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341" \
    -b \
    "010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341" \
    -f wkb \
    intersection

Notre résultat est : 0104000000020000000101000000A899EFC8C83C3E4175E5698166D553410101000000B5EBDD9E8F3C3E416BF8515379D55341

Vous comprendrez mieux l'opération qui va suivre grâce à la lecture de l'article sur le WKT et WKB³. En attendant, je vous demande de me faire confiance .

En attendant l'article WKT/B : décomposer un WKB

Lorsque l'on lit le WKB d'un multipoint comme celui-ci 0104000000020000000101000000A899EFC8C83C3E4175E5698166D553410101000000B5EBDD9E8F3C3E416BF8515379D55341, on voit... que dalle ! Hum certes.
Allez, prenez un peu de géo-collyre et à y regarder de plus près, on y distingue nos deux points dedans, chacun "préfixé" par 0101000000 (le 01 pour Little endian¹ et 01000000 pour indiquer que c'est un point 2D) :

0101000000 A899EFC8C83C3E4175E5698166D55341
0101000000 B5EBDD9E8F3C3E416BF8515379D55341

Ce qui équivaut, moyennant la différence, sans conséquence, entre majuscules et minuscules, à :

0101000000``a899efc8c83c3e4175e5698166d55341
0101000000``b5ebdd9e8f3c3e416bf8515379d55341

Ainsi, on peut continuer de décomposer le WKB pour obtenir les coordonnées du premier point 0101000000``A899EFC8C83C3E4175E5698166D55341 qui, une fois le "préfixe" 0101000000 retiré, est une paire de 16 caractères :

a899efc8c83c3e41
75e5698166d55341

Très bien. Est-ce que le point intersecte ou touche une des géométries d'origine ?

> geosop \
-a \
"0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341" \
-b \
"0104000000020000000101000000A899EFC8C83C3E4175E5698166D553410101000000B5EBDD9E8F3C3E416BF8515379D55341" \
intersects

Ici, je teste si le multipoint intersecte la géométrie base. Cela retourne faux.

De même entre le multipoint et line :

> geosop \
-a \
"010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341" \
-b \
"0104000000020000000101000000A899EFC8C83C3E4175E5698166D553410101000000B5EBDD9E8F3C3E416BF8515379D55341" \
intersects

Vous pouvez également essayer directement avec les points 0101000000A899EFC8C83C3E4175E5698166D55341 et 0101000000B5EBDD9E8F3C3E416BF8515379D55341, plutôt que le multipoint. De même, vous pouvez tester les autres prédicats comme touches, le résultat sera toujours false... Sauf pour... disjoint ce qui veut dire que les points ne sont pas sur les géométries.

Alors pourquoi, si les points ne sont pas sur les lignes, nous avions sur QGIS des segments qui intersectaient la géométrie d'origine ?

Si vous êtes attentif, vous pouvez remarquer qu'un côté des deux, seulement, avait une intersection ; et ce n'était pas toujours le même. Je vous laisse regarder les images de la partie précédente.

On commence à toucher du doigt le problème. Le point d'intersection est d'un côté ou de l'autre du segment. Si l'on était sur un hyper zoom, on aurait quelque chose comme :

En simplifiant, on pourrait dire que les points sont sur de minuscules grilles. Le point n'est pas sur la ligne, mais très proche.

D'ailleurs, demandons à GEOS où se trouvent les points sur nos géométries d'origine.

La distance du premier point par rapport à la base :

> geosop \
-a \
"0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341" \
-b \
"0101000000A899EFC8C83C3E4175E5698166D55341" \
distance

3.356426828584339e-10

Le second point :

> geosop \
-a \
"0102000000050000007997c6b68d3c3e4139eb62c260d55341ac9ea7316a3c3e41cbeb40e073d55341403e0bfbc33c3e41b3fc06f380d55341387a2a800c3d3e41f256b8176dd553417997c6b68d3c3e4139eb62c260d55341" \
-b \
"0101000000B5EBDD9E8F3C3E416BF8515379D55341" \
distance

3.0508414550559678e-10

La distance du premier point par rapport à line :

> geosop \
-a \
"010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341" \
-b \
"0101000000A899EFC8C83C3E4175E5698166D55341" \
distance

1.812697635977354e-10

Le second point :

> geosop \
-a \
"010200000002000000ea9c6d2b873c3e41a03d941b7cd5534133db7796ce3c3e413fba569864d55341" \
-b \
"0101000000B5EBDD9E8F3C3E416BF8515379D55341" \
distance

1.7234470954287178e-10

On remarque que le résultat n'est pas 0, mais très proche. C'est en gros 0, mais y'a une « blague » vers 10 chiffres après la virgule. Pour celles et ceux que cela intéresse, je reviendrai sur l'importance du calcul dans la partie algorithme. En attendant, on observe que QGIS donne le même résultat que GEOS. Ce qui n'est pas étonnant puisque derrière QGIS ², c'est GEOS.

C'est donc GEOS qui est faux ? Non, GEOS donne le « bon » résultat, mais la vérité est ailleurs. Nous continuerons cette exploration dans les parties suivantes.

3 : GRASS et SAGA

Auteur·ice#

Loïc Bartoletti #

Après un cursus en Histoire, je me suis orienté vers l'urbanisme sur l'aménagement des territoires.

J'ai travaillé pendant environ 10 ans dans une station touristique dans les Alpes, Megève, en tant qu'urbaniste puis responsable du bureau d'études et administrateur SIG.

Bidouilleur et partisan des solutions OpenSource, j'ai commencé à toucher à GRASS, puis QGIS et PostGIS. Au fil du temps j'ai contribué à ces logiciels, principalement pour migrer des outils DAO vers le SIG et je suis aujourd'hui commiter QGIS, PostGIS et FreeBSD où je m'occupe des paquets des outils OSGeo et plus si affinité.

Licence Beerware #

Ce contenu est sous licence Beerware (Révision 42).
Les médias d'illustration sont potentiellement soumis à d'autres conditions d'utilisation.

Réutiliser, citer l'article

Tant que vous conservez cette licence :

vous pouvez faire ce que vous voulez de ce contenu
si vous rencontrez l'auteur/e un jour et que vous pensez que ce contenu vaut le coup, vous pouvez lui payer un coup en retour

Citer cet article :

"GEOS au cœur de QGIS" publié par Loïc Bartoletti sur Geotribu - Source : https://geotribu.fr/articles/2024/2024-07-25_de-la-tolerance-en-sig-geometrie-02-qgis-et-geos/

ou en Français, gros- et petit-boutisme, sont l'ordre dans lequel les octets sont placés. Pour plus d'informations, je vous invite à regarder la page Wikipedia ↩
Comme expliqué avant, QGIS réalise certains calculs, identiques à ceux de GEOS, pourtant sans utiliser cette bibliothèque. En particulier, l'accrochage ne repose pas sur GEOS, mais sur des calculs équivalents. Je simplifie ici pour éviter de perdre les moins connaisseurs de cet écosystème. ↩
formats standards de représentation des géométries :
- WKB (Well-Known Binary) : Le WKB est un format binaire utilisé pour représenter des objets géométriques de manière compacte et efficace, couramment utilisé dans les bases de données géospatiales pour le stockage et l'échange de données géographiques.
- WKT (Well-Known Text) : Le WKT est un format texte utilisé pour représenter des objets géométriques de manière lisible par l'humain. Il est souvent utilisé pour le partage et l'affichage de données géographiques.
Pour plus d'informations, consultez la page Wikipedia. ↩↩

Commentaires

Afin de favoriser les échanges constructifs, merci de préférer le pseudonymat à l'anonymat. Pour rappel, l'adresse mail n'est pas exposée publiquement et sert principalement aux notifications de réponse. Les commentaires sont automatiquement republiés sur nos réseaux sociaux pour favoriser la discussion. Consulter la page sur la confidentialité et les données personnelles.
Une version minimale de la syntaxe markdown est acceptée pour la mise en forme des commentaires.
Propulsé par Isso.

Ce contenu est sous licence Beerware Pictogramme BeerWare